Fungsi Invers dan Fungsi Komposisi

1. Nilai Fungsi Komposisi dan Komponen Pembentuknya

Untuk menjelaskan nilai fungsi komposisi terhadap komponen pembentuknya, dapat dilakukan dengan dua cara berikut ini.

1. Dengan menentukan rumus komposisinya terlebih dahulu, kemudian disubstitusikan 
nilainya.
2. Dengan mensubstitusikan secara langsung nilai pada fungsi yang akan dicari.

Untuk lebih memahami, perhatikan contoh soal berikut ini.

Contoh soal

Diketahui dua buah fungsi yang dinyatakan dengan rumus f(x) = 3x – 1 dan g(x) = x2 + 4. Tentukanlah nilai dari fungsi-fungsi komposisi berikut.


a. (gcf)(1)


b. (f c g)(–2)

c. (gcf)(–3)

Penyelesaian


Cara 1

a. (g._0.f)(x)     = g(f(x))


= g(3x – 1)


= (3x – 1)2 + 4


= 9x²–6x+1+4

= 9x² – 6x + 5

(g.0.f)(1)    = 9⋅12 –6⋅1+5

= 9–6+5=8

b. (f.0.g)(–2)   = f(g(x))


= f(x2+4)

= 3(x2+4)–1

= 3×2+12–1


= 3×2+11

(f.0.g)(–2)
   = 3(–2)2 + 11


= 3⋅4+11


= 12+11 = 23

c. (g.0.f)(x)       = 9×2–6x+5

(g.0.f)(–3)     = 9(–3)2 – 6 (–3) + 5

= 81+18+5

= 104

Cara 2
a.(g.0.f)(1)     = g(f(1))

= g(3⋅1–1)

= g(2)


= 22 + 4

= 8

b. (f.0.g) (–2) = f(g(–2))

=  f((–2)2 + 4)

=  f(8)

=  3⋅8–1 = 23

c. (g.0.f)(–3) =
 g(f(–3))

= g(3 (–3) – 1)

= g(–10)

= (–10)2 +4

= 104

 2. INVERS merupakan materi yang berkaitan dengan fungsi jadi materi prasyarat dalam mempelajari materi ini adalah sudah terlebih dahulu menguasai berbagai macam bentuk fungsi seperti fungsi linier, fungsi kuadrat, fungsi irasional dan sebagainya.

Jadi, invers suatu fungsi f dapat didefinisikan sebagai berikut:

Jika fungsi  f : A --->B  dinyatakan dengan pasangan berurutan

Maka invers dari fungsi f adalah f^-1 : B --->A ditentukan dengan

Catatan:

(1). Invers suatu fungsi belum tentu merupakan fungsi

(2). Jika invers suatu fungsi adalah fungsi maka invers fungsi tersebut disebut fungsi invers.

Untuk memperjelas catatan diatas perhatikan ilustrasi dalam diagram panah dibawah ini:

Perhatikan gambar (1.a) fungsi f merupakan pemetaan / fungsi, tetapi dari gambar (1.b) tampak bahwa f ^-1 merupakan relasi biasa ( bukan pemetaan / fungsi ), karena ada dua pasangan terurut yang mempunyai ordinat yang sama yaitu, (1,a) dan (1,b). Jadi, f ^-1 adalah invers fungsi bukan fungsi invers.

Sekarang perhatikan gambar (2.a), f merupakan pemetaan / fungsi. Dan dari gambar (2.b), f ^-1 juga merupakan fungsi. Jadi, f ^-1 adalah fungsi invers.

Sekarang kita sudah mendapatkan gambaran tentang definisi fungsi invers matematika, maka dari gambar (1) dan gambar (2) dapat ditarik kesimpilan bahwa:

Suatu fungsi f : A ---> B mempunyai fungsi invers f ^-1 : B ---->A jika dan hanya jika f merupakan fungsi bijektif atau himpunan A dan B dalam korespondensi satu-satu.      (Sartono Wirodikromo, Matematika SMA. Jakarta : Erlangga).

Cara menentukan rumus fungsi invers matematika

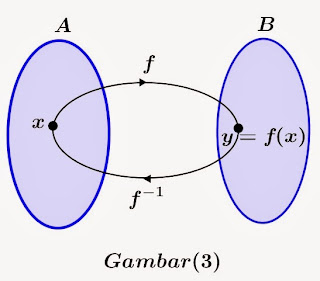
Jika f merupakan fungsi bijektif atau korespondensi satu-satu, maka invers dari fungsi f atau f ^-1 adalah fungsi invers. Coba perhatikan gambar (3) dibawah ini:

Dari gambar (3), jika f merupakan fungsi bijektif dan y adalah bayangan (peta) dari x maka,

Jika f ^-1 adalah invers fungsi f , maka x adalah peta dari y oleh f  ^-1 dapat dinyatakan dengan

Langkah-Langkah Menentukan Fungsi invers matematika 

 

Dari uraian diatas dapat diperoleh langkah-langkah menentukan fungsi invers matematika, yaitu sebagai berikut:

(1) Ubahlah persamaan bentuk y = f (x) dalam bentuk x sebagi fungsi y

(2) Bentuk x sebagai fungsi y pada langkah (1) di beri nama f ^-1 (y)

(3) Ubahlah y pada pada bentuk  f ^-1 (y) dengan x untuk mendapatkan f ^-1 (x). f ^-1 (x) yang diperoleh adalah rumus fungsi invers dari f(x).

Supaya lebih memahami dan mampu menyelesaikan cara menentukan fungsi invers matematika, perhatikan contoh-contoh berikut ini:

Contoh 1 :

Tentukan rumus fungsi invers  dari  , y = 3 x + 6

[Penyelesaian]

y = 3 x + 6

Bentuk x sebagai fungsi dalam y,

Contoh 2 :

Tentukanlah rumus fungsi invers dari,  y = x³ - 1

[Penyelesaian]

Cara menentukan rumus fungsi invers matematika untuk soal diatas adalah, ubah terlebih dahulu ke bentuk x sebagai fungsi y  yaitu :

y = x³ - 1

Bentuk x sebagai fungsi dalam y,

Ada cara lain dalam menentukan rumus fungsi invers matematika suatu fungsi yaitu dengan menukar variabel nya.

Contoh 3 :

Tentukanlah rumus fungsi invers dari ,

[PenyelesaianG]

Tukarlah x dan y, maka

Susunlah kembali,

Contoh 4 :

Carilah rumus fungsi invers untuk,

[Penyelesaian]

Bentuk x sebagai fungsi dalam y,

Bagaimana menentukan rumus fungsi invers matematika jika fungsinya bukan merupakan fungsi bijektif? Maka harus diusahakan agar fungsi tersebut menjadi fungsi bijektif dengan cara membatasi domain alaminya. Perhatikan contoh soal dibawah ini!

Contoh 5 :

Diketahui fungsi f dengan rumus, f(x) = (x+1)², tentukan rumus fungsi inversnya!

[Penyelesaian]

f(x) = (x+1)² adalah fungsi kuadrat dengan domain f, D_f = {x | x anggota R}, jika digambar grafiknya sebagai berikut :

Dari grafik diatas , agar f(x) = (x+1)² mempunyai invers maka domainya harus dibatasi yaitu,

 Perhatikan gambar dibawah ini untuk masing-masing domain:

Perhatikan gambar (b) dan gambar (c) diatas, dengan membatasi domain alami dari fungsi f(x) = (x+1)², maka fungsi tersebut menjadi fungsi bijektif. Maka cara menentukan fungsi invers matematika, f(x) = (x+1)² adalah:

Seperti itulah cara menentukan fungsi invers matematika jika fungsinya bukan fungsi bijektif, yaitu dengan membatasi domain alaminya.

Contoh 6 :

Tentukan rumus fungsi invers jika,

[Penyelesaian]

Untuk contoh soal berikut ini, adalah bagaimana mencari fungsi f (x ), jika diketahui f ^-1(x ). Tentu caranya sama saja seperti menentukan fungsi invers matematika.

Contoh 7 :

Tentukan f (x), jika diketahui,

[Penyelesaian]

Dari contoh-contoh soal yang diberikan diatas anda diharapkan terampil dalam menyelesaikan soal-soal yang berkaitan dengan cara menentukan fungsi invers matematika.