Aku ini manusia dan kalian tidak tahu kesedihanku
Mungkin aku tertawa tapi bayanganku menjerit
Aku ini seorang gadis yang melalang buana mencari kaca yang paling pas untuk hidupku
Saat malam berkunjung aku hanya bisa menatap langit dan menyapa bintang
bulan.. sedang apakah dirimu yang selalu tersenyum
aku bukan siapa siapa tapi aku tau Tuhan selalu mencintaiku
Saat aku sadara betapa ndahnya hidup ini
saat itu pula aku tahu arti dari kejamnya kehidupan
aku hanya mampu mengucapkan seutas kata kata lirih
damai untuk pikiranku
keseimbangan untuk hidupku
cinta untuk hatiku
kebahagiaan untuk batinku
dan rasa sakit untuk pengalamanku
main |
sidebar
Operasi yang digunakan adalah
1. Negasi Tabel kebenaran untuk TIDAK p (juga ditulis ¬p, Np, Fpq, or ~p) adalah dibawah ini:
2. Konjungsi
Tabel kebenaran untuk p DAN q (juga ditulis p ∧ q, Kpq, p & q, atau p  q) adalah dibawah ini:
q) adalah dibawah ini:
3. Disjungsi inklusif (sering disebut sebagai disjungsi saja)
Tabel kebenaran untuk p ATAU q (juga ditulis p ∨ q, Apq, p || q, or p + q) adalah dibawah ini:
4. Kesamaan
Tabel kebenaran untuk p XNOR q (juga ditulis p ↔ q, Epq, p = q, or p ≡ q) adalah dibawah ini:
5. Disjungsi eksklusif
Tabel kebenaran untuk p XOR q (juga ditulis p ⊕ q, Jpq, or p ≠ q) adalah dibawah ini:
a.(g.0.f)(1) = g(f(1))
b. (f.0.g) (–2) = f(g(–2))
c. (g.0.f)(–3) = g(f(–3))


Perhatikan gambar (1.a) fungsi f merupakan pemetaan / fungsi, tetapi dari gambar (1.b) tampak bahwa f -1 merupakan relasi biasa ( bukan pemetaan / fungsi ), karena ada dua pasangan terurut yang mempunyai ordinat yang sama yaitu, (1,a) dan (1,b). Jadi, f -1 adalah invers fungsi bukan fungsi invers.


y = 3 x + 6


















Dari
contoh-contoh soal yang diberikan diatas anda diharapkan terampil dalam menyelesaikan
soal-soal yang berkaitan dengan cara menentukan fungsi invers matematika.
himpunan B pada gambar tersebut adalah untuk setiap x anggota A dipetakan
ke (x + 1) anggota B. Suatu fungsi dinotasikan dengan huruf kecil, seperti f,
g, atau h. Jika fungsi pada Gambar 2.5 dinamakan f maka fungsi tersebut
dinotasikan dengan f: x x + 1 (dibaca: fungsi f memetakan x ke x + 1).
Dengan demikian, pada pemetaan f: x x + 1 dari himpunan A ke himpunan
B diperoleh.
Untuk x = 1, f: 1 1 + 1 atau f: 1 2 sehingga (1, 2) f,
Untuk x = 2, f: 2 2 + 1 atau f: 2 3 sehingga (2, 3) f,
Untuk x = 3, f: 3 3 + 1 atau f: 3 4 sehingga (3, 4) f.
Untuk memudahkan cara menulis atau membaca, suatu pemetaan dapat dituliskan dalam bentuk tabel atau daftar. Untuk fungsi f : x x + 1, tabelnya adalah sebagai berikut.
Dengan menggunakan pasangan-pasangan berurutan yang diperoleh pada Tabel 2.6 dapat digambar grafik Cartesius untuk fungsi f: x → x + 1 seperti tampak pada Gambar 2.6 . Gambar 2.6 merupakan grafik Carteius fungsi f: x → x + 1 dengan
domain Df = A = {1, 2, 3,}, kodomain B = {1, 2, 3, 4} dan Range Rf = {2, 3, 4} yang digambarkan dengan noktah-noktah. Jika domain dan kodomainnya diperluas pada himpunan bilangan riil, rangenya ditunjukkan dengan garis yang melalui noktah-noktah seperti pada Gambar 2.6.
2. Menghitung Nilai Fungsi
Pada bagian ini, kamu akan mempelajari cara menghitung nilai fungsi. Pelajarilah contoh-contoh soal berikut.
3. Menentukan Rumus fungsi
Suatu fungsi dapat ditentukan rumusnya jika nilai data diketahui.
Bagaimanakah caranya? Untuk menjawabnya, pelajarilah contoh soal
berikut.
Sabtu, 05 Juli 2014
Tulisan Bebas : Aku Tau
Diposting oleh Unknown di 03.49Tabel Kebenaran
Diposting oleh Unknown di 03.45
Tabel kebenaran adalah tabel dalam matematika yang digunakan
untuk melihat nilai kebenaran dari suatu premis/pernyataan. Jika hasil akhir
adalah benar semua (dilambangkan B, T, atau 1), maka disebut tautologi.
Sedangkan jika salah semua (S, F, atau 0) disebut kontradiksi. Premis yang hasil
akhirnya gabungan benar dan salah disebut kontingensi.
Operasi yang digunakan adalah
1. Negasi Tabel kebenaran untuk TIDAK p (juga ditulis ¬p, Np, Fpq, or ~p) adalah dibawah ini:
| p | ¬p |
|---|---|
| S | B |
| B | S |
| p | q | p ∧ q |
|---|---|---|
| B | B | B |
| B | S | S |
| S | B | S |
| S | S | s |
| p | q | p ∨ q |
|---|---|---|
| B | B | B |
| B | S | B |
| S | B | B |
| S | S | S |
| p | q | p ≡ q |
|---|---|---|
| B | B | B |
| B | S | S |
| S | B | S |
| S | S | B |
| p | q | p ⊕ q |
|---|---|---|
| B | B | S |
| B | S | B |
| S | B | B |
| S | S | S |
Fungsi Invers dan Fungsi Komposisi
Diposting oleh Unknown di 03.44
1. Nilai Fungsi Komposisi dan Komponen Pembentuknya
Untuk menjelaskan nilai fungsi komposisi terhadap komponen pembentuknya, dapat dilakukan dengan dua cara berikut ini.
- Dengan menentukan rumus komposisinya terlebih dahulu, kemudian disubstitusikan nilainya.
- Dengan mensubstitusikan secara langsung nilai pada fungsi yang akan dicari.
Untuk lebih memahami, perhatikan contoh soal berikut ini.
Contoh soal
Diketahui
dua buah fungsi yang dinyatakan dengan rumus f(x) = 3x – 1 dan g(x) = x2
+ 4. Tentukanlah nilai dari fungsi-fungsi komposisi berikut.
a. (gcf)(1)
b. (f c g)(–2)
c. (gcf)(–3)
Penyelesaian
Cara 1
a. (g.0.f)(x) = g(f(x))
= g(3x – 1)
= (3x – 1)2 + 4
= 9x2–6x+1+4
= 9x2 – 6x + 5
(g.0.f)(1) = 9⋅12 –6⋅1+5
= 9–6+5=8
b. (f.0.g)(–2) = f(g(x))
= f(x2+4)
= 3(x2+4)–1
= 3×2+12–1
= 3×2+11
(f.0.g)(–2)
= 3(–2)2 + 11
= 3⋅4+11
= 12+11 = 23
c. (g.0.f)(x) = 9×2–6x+5
(g.0.f)(–3) = 9(–3)2 – 6 (–3) + 5
= 81+18+5
= 104
Cara 2a.(g.0.f)(1) = g(f(1))
= g(3⋅1–1)
= g(2)
= 22 + 4
= 8
b. (f.0.g) (–2) = f(g(–2))
= f((–2)2 + 4)
= f(8)
= 3⋅8–1 = 23
c. (g.0.f)(–3) = g(f(–3))
= g(3 (–3) – 1)
= g(–10)
= (–10)2 +4
= 104
2. INVERS merupakan materi yang berkaitan dengan
fungsi jadi materi prasyarat dalam mempelajari materi ini adalah sudah terlebih
dahulu menguasai berbagai macam bentuk fungsi seperti fungsi linier, fungsi
kuadrat, fungsi irasional dan sebagainya.
Jadi,
invers suatu fungsi f dapat didefinisikan sebagai berikut:
Jika
fungsi f : A --->B dinyatakan dengan pasangan berurutan
Maka
invers dari fungsi f adalah f-1 : B --->A ditentukan dengan
Catatan:
(1).
Invers suatu fungsi belum tentu merupakan fungsi
(2).
Jika invers suatu fungsi adalah fungsi maka invers fungsi tersebut disebut fungsi invers.
Perhatikan gambar (1.a) fungsi f merupakan pemetaan / fungsi, tetapi dari gambar (1.b) tampak bahwa f -1 merupakan relasi biasa ( bukan pemetaan / fungsi ), karena ada dua pasangan terurut yang mempunyai ordinat yang sama yaitu, (1,a) dan (1,b). Jadi, f -1 adalah invers fungsi bukan fungsi invers.
Sekarang
perhatikan gambar (2.a), f merupakan pemetaan / fungsi. Dan dari gambar (2.b),
f -1 juga merupakan fungsi. Jadi, f -1 adalah fungsi
invers.
Sekarang
kita sudah mendapatkan gambaran tentang definisi fungsi invers matematika, maka dari gambar (1) dan gambar (2)
dapat ditarik kesimpilan bahwa:
Suatu
fungsi f : A ---> B mempunyai
fungsi invers f -1 : B ---->A
jika dan hanya jika f merupakan
fungsi bijektif atau himpunan A dan B dalam korespondensi satu-satu. (Sartono Wirodikromo, Matematika SMA. Jakarta : Erlangga).
Cara
menentukan rumus fungsi invers matematika
Jika
f merupakan fungsi bijektif atau korespondensi satu-satu, maka invers dari
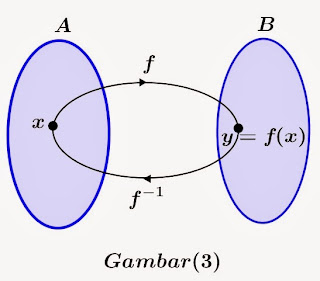
fungsi f atau f -1 adalah fungsi invers. Coba perhatikan gambar (3)
dibawah ini:
Dari
gambar (3), jika f merupakan fungsi bijektif dan y adalah bayangan (peta) dari
x maka,
Jika
f -1 adalah invers fungsi f , maka x adalah peta dari y oleh f -1
dapat dinyatakan dengan
Langkah-Langkah Menentukan Fungsi invers matematika
Dari
uraian diatas dapat diperoleh langkah-langkah menentukan fungsi invers
matematika, yaitu sebagai berikut:
(1)
Ubahlah persamaan bentuk y = f (x) dalam bentuk x sebagi fungsi y
(2)
Bentuk x sebagai fungsi y pada langkah (1) di beri nama f -1 (y)
(3)
Ubahlah y pada pada bentuk f -1
(y) dengan x untuk mendapatkan f -1 (x). f -1 (x) yang
diperoleh adalah rumus fungsi invers dari f(x).
Supaya
lebih memahami dan mampu menyelesaikan cara menentukan fungsi invers
matematika, perhatikan contoh-contoh berikut ini:
Contoh
1 :
Tentukan
rumus fungsi invers dari , y = 3 x + 6
[Penyelesaian]
Bentuk
x sebagai fungsi dalam y,
Contoh
2 :
Tentukanlah
rumus fungsi invers dari, y = x3 - 1
[Penyelesaian]
Cara
menentukan rumus fungsi invers matematika untuk soal diatas adalah, ubah
terlebih dahulu ke bentuk x sebagai fungsi y
yaitu :
y = x3 - 1
y = x3 - 1
Bentuk
x sebagai fungsi dalam y,
Ada
cara lain dalam menentukan rumus fungsi invers matematika suatu fungsi yaitu dengan
menukar variabel nya.
Contoh
3 :
Tentukanlah
rumus fungsi invers dari ,

[PenyelesaianG]
Tukarlah
x dan y, maka
Susunlah
kembali,
Contoh
4 :
Carilah
rumus fungsi invers untuk,

[Penyelesaian]

Bentuk
x sebagai fungsi dalam y,
Bagaimana
menentukan rumus fungsi invers matematika jika fungsinya bukan merupakan fungsi
bijektif? Maka harus diusahakan agar
fungsi tersebut menjadi fungsi bijektif dengan cara membatasi domain alaminya.
Perhatikan contoh soal dibawah ini!
Contoh 5 :
Diketahui
fungsi f dengan rumus, f(x) = (x+1)2, tentukan rumus fungsi
inversnya!
[Penyelesaian]
f(x)
= (x+1)2 adalah fungsi kuadrat dengan domain f, Df = {x |
x anggota R}, jika digambar grafiknya sebagai berikut :
Dari
grafik diatas , agar f(x) = (x+1)2 mempunyai invers maka domainya harus
dibatasi yaitu,
Perhatikan
gambar (b) dan gambar (c) diatas, dengan membatasi domain alami dari fungsi
f(x) = (x+1)2, maka fungsi tersebut menjadi fungsi bijektif. Maka
cara menentukan fungsi invers matematika, f(x) = (x+1)2 adalah:
Seperti
itulah cara menentukan fungsi invers matematika jika fungsinya bukan fungsi
bijektif, yaitu dengan membatasi domain alaminya.
Contoh 6 :
Tentukan
rumus fungsi invers jika,

[Penyelesaian]
Untuk
contoh soal berikut ini, adalah bagaimana mencari fungsi f (x ), jika diketahui
f -1(x ). Tentu caranya sama saja seperti menentukan fungsi invers matematika.
Contoh 7 :
Tentukan
f (x), jika diketahui,

[Penyelesaian]
Pernyataan dan Bukan Pernyataan, Negasi, Implikasi, Tautologi dan Kontradiksi
Diposting oleh Unknown di 03.35- Kalimat pernyataan atau bukan pernyataan
Dalam matematika dikenal dua jenis kalimat yaitu kalimat tertutup (bukan pernyataan) atau kalimat terbuka (pernyataan)
1. kalimat terbuka / bukan pernyataan
kalimat terbuka ialah suatu kalimat yang
memuat variable, nilai kebenarannya belum dapat ditentukan, apabila
bernilai salah atau benar.
Contah:
X adalah factor dari 15
P adalah bilangan rasional
Buktikan bahwa sin2x + cos2x = 1
2.kalimat tertutup/ bukan pernyataan
pernyataan adalah suatu kalimat yang
dapat ditentukan nilai kebenarannya, yaitu benar atau salah, tetapi
tidak dapat terjadi benar atau salah bersamaan.
Untuk menentukan nilai kebenaran suatu pernyataan ada dua dasar, yaitu:
A. Dasar empiris
kebenaran suatu pernyataanditentukan pada
saat itu. Beasanya diadakan pengamataan lebih dahulu. Jadi, nilai
kebenarannya bersifat relative
contoh:
- budi sakit perut
- bapak kepala sekolah berambut putih
- kota Jakarta terkena bencana banjir
B. Dasar tak empiris
kebenaran suau pernyataan bersifat mutlak, tidak tergantung pada waktu dan tempat.
Contoh:
- 4 adalah bilangan genap
- setahun ada 12 bulan
- 32 = 9
2. Negasi
Dalam logika matematika , negasi atau
ingkaran adalah operasi matematika terhadap suatu pernyataan baik
tunggal maupun majemuk. Operasi negasi membalikkan nilai kebenaran suatu
pernyataan. Jika suatu pernyataan p benar, maka negasinya p salah, dan
jika sebaliknya pernyataan p salah, maka negasinya p benar
Contoh-
P : Hasil ulangan ilmu hitung keuangan budi adalah 9
~ p : Hasil ulangan ilmu hitung keuangan budi adalah bukan 9
Secara umum bahwa negasi suatu pernyataan
adalah pernyataan lain yang bernilai salah, jika pernyataan awalnya
bernilai benar dan akan bernilai benar jika awalanya bernilai salah.
3. Konjungsi
Konjungsi adalah cara menghubungkan dua
pernyataan dengan menggunakan kata ‘atau’. Konjungsi bernilai salτah
jika paling tidak ada salah satu pernyataan yang salah dan hanya
bernilai benar jika semua pernyataan benar. Konjungsi dilambangkan
dengan ∧
Contoh:
p: 1+1=2 (benar)
j: 4 adalah bilangan genap (Benar)
τ (p ∧ j) = Benar
p: 1+1=2 (Benar)
j: 5 adalah bilangan genap (Salah)
τ (p ∧ j) = Salah
4. Implikasi
Implikasi yang juga disebut pernyataan
bersyarat/ kondisional adalah pernyataan yang disusun dari 2 pernyataan
dengan bentuk jika … maka … . Implikasi dilambangkan dengan ⇒. Implikasi
tidak berlaku sebaliknya (p⇒q tidak sama dengan q⇒p).
| Pernyataan | p | q | p ⇒ q | q ⇒ p |
| B | B | B | B | |
| B | S | S | B | |
| S | B | B | S | |
| S | S | B | B |
5. Biimplikasi
Bimplikasi yang juga disebut pernyataan
bersyarat/ kondisional adalah pernyataan yang disusun dari 2 pernyataan
dengan bentuk … jika dan hanya jika … . Bimplikasi dilambangkan dengan
⇔. Tidak seperti implikasi, biimplikasi bersifat 2 arah/ bisa dibalik
(p⇔q sama dengan q⇔p).
| Pernyataan | p | q | p ⇔ q | q ⇔ p |
| B | B | B | B | |
| B | S | S | S | |
| S | B | S | S | |
| S | S | B | B |
Negasi, disjungsi, konjungsi, implikasi, dan biimplikasi juga dapat disatukan dalam suatu persoalan.
Contoh soal: Cari τ[~(p ∨ ~q)]
| Pernyataan | p | q | p ⇒ q | (p ⇒ q) ^ p |
{(p ⇒ q) ^ p}⇒ q |
| B | B | B | B | B | |
| B | S | S | S | B | |
| S | B | B | S | B | |
| S | S | B | S | B |
Maka τ[{(p ⇒ q) ^ p}⇒q] = B B B B
6. TAUTOLOGI
Tautologi adalah pernyataan majemuk yang selalu benar
untuk semua kemungkinan nilai kebenaran dari pernyataan-pernyataan
komponennya. Sebuah Tautologi yang memuat pernyataan Implikasi disebut
Implikasi Logis. Untuk membuktikan apakah suatu pernyataan Tautologi,
maka ada dua cara yang digunakan. Cara pertama dengan menggunakan tabel
kebenaran, yaitu jika semua pilihan bernilai B (benar) maka disebut
Tautologi, dan cara kedua yaitu dengan melakukan penjabaran atau
penurunan dengan menerapkan sebagian dari 12 hukum-hukum Ekuivalensi
Logika.
Contoh tautologi dengan menggunakan tabel kebenaran:
1. (p ʌ~q) p
Pembahasan:
| p | q | ~q | (p ʌ~q) | (p ʌ ~q) p |
| B
B S S |
B
S B S |
S
B S B |
S
B S S |
B
B B B |
Ini adalah tabel kebenaran yang
menunjukkan Tautologi dengan alasan yaitu semua pernyataannya bersifat
benar atau True (T). maka dengan perkataan lain pernyataan majemuk (p ʌ
~q) p selalu benar.
7. KONTRADIKSI
Kontradiksi adalah kebalikan dari
tautologi yaitu suatu bentuk pernyataan yang hanya mempunyai contoh
substansi yang salah, atau sebuah pernyataan majemuk yang salah dalam
segala hal tanpa memandang nilai kebenaran dari komponen-komponennya.
Untuk membuktikan apakah suatu pernyataan tersebut kontradiksi, maka ada
dua cara yang digunakan. Cara pertama dengan menggunakan tabel
kebenaran, yaitu jika semua pilihan bernilai F atau salah maka disebut
kontradiksi, dan cara kedua yaitu dengan melakukan penjabaran atau
penurunan dengan menerapkan sebagian dari 12 hukum-hukum Ekuivalensi
Logika.[1][4][4]
Contoh dari Kontradiksi:
1. (A ʌ~A)
Pembahasan:
| A | ~A | (A ʌ~A) |
| B S | S B | S S |
Dari tabel kebenaran diatas dapatlah disimpulkan bahwa pernyataan majemuk (A ʌ~A) selalu salah.
2. P ʌ (~p ʌ q)
Pembahasan:
| p | q | ~p | (~p ʌ q) | P ʌ (~p ʌ q) |
| B
B S S |
B
S B S |
S
S B B |
S
S B S |
S
S S S |
Ini adalah tabel kebenaran yang menunjukkan kontradiksi dengan alasan yaitu semua pernyataan bernilai salah (F).
DEFINISI FUNGSI (DOMAIN , KODOMAIN , RANGE)
Diposting oleh Unknown di 03.30
- Fungsi atau pemetaan adalah relasi khusus yang memasangkan setiap
anggota satu himpunan dengan tepat satu anggota satu himpunan yang lain.
Domain, Kodomain, dan Range Fungsi
- 2 B merupakan peta dari 1 A
- 3 B merupakan peta dari 2 A
- 4 B merupakan peta dari 3 A
- Domainnya (Df) adalah A = {1, 2, 3}.
- Kodomainnya adalah B = {1, 2, 3, 4}.
- Rangenya (Rf) adalah {2, 3, 4}.
| Contoh Soal :
Perhatikan diagram panah berikut. Diagram panah tersebut menunjukkan fungsi himpunan P ke himpunan Q dengan relasi "dua kali dari". Tentukanlah domain, kodomain, dan range fungsinya. Jawab : • Domainnya (Df) adalah P = {4, 6, 8, 10} • Kodomainnya adalah Q = {1, 2, 3, 4, 5} • Rangenya (Rf) adalah {2, 3, 4, 5} |
- Grafik Fungsi
himpunan B pada gambar tersebut adalah untuk setiap x anggota A dipetakan
ke (x + 1) anggota B. Suatu fungsi dinotasikan dengan huruf kecil, seperti f,
g, atau h. Jika fungsi pada Gambar 2.5 dinamakan f maka fungsi tersebut
dinotasikan dengan f: x x + 1 (dibaca: fungsi f memetakan x ke x + 1).
Dengan demikian, pada pemetaan f: x x + 1 dari himpunan A ke himpunan
B diperoleh.
Untuk x = 1, f: 1 1 + 1 atau f: 1 2 sehingga (1, 2) f,
Untuk x = 2, f: 2 2 + 1 atau f: 2 3 sehingga (2, 3) f,
Untuk x = 3, f: 3 3 + 1 atau f: 3 4 sehingga (3, 4) f.
Untuk memudahkan cara menulis atau membaca, suatu pemetaan dapat dituliskan dalam bentuk tabel atau daftar. Untuk fungsi f : x x + 1, tabelnya adalah sebagai berikut.
Dengan menggunakan pasangan-pasangan berurutan yang diperoleh pada Tabel 2.6 dapat digambar grafik Cartesius untuk fungsi f: x → x + 1 seperti tampak pada Gambar 2.6 . Gambar 2.6 merupakan grafik Carteius fungsi f: x → x + 1 dengan
domain Df = A = {1, 2, 3,}, kodomain B = {1, 2, 3, 4} dan Range Rf = {2, 3, 4} yang digambarkan dengan noktah-noktah. Jika domain dan kodomainnya diperluas pada himpunan bilangan riil, rangenya ditunjukkan dengan garis yang melalui noktah-noktah seperti pada Gambar 2.6.
| Contoh Soal :
Gambarlah grafik fungsi f: x → 2x pada bidang Cartesius dengan domain dan kodomainnya himpunan bilangan riil. Jawab : Terdapat beberapa langkah untuk menggambarkan suatu grafik fungsi, sebagai berikut. (1) Tentukan domainnya. Untuk memudahkan, ambil beberapa bilangan bulat di sekitar nol. (2) Buat tabel pasangan berurutan fungsi tersebut. (3) Gambarkan noktah-noktah pasangan berurutan tersebut pada bidang Cartesius. Kemudian, hubungkan noktah-noktah itu dengan garis lurus sehingga diperoleh grafik seperti pada gambar berikut. |
1. Notasi Fungsi
Pada bagian sebelumnya, kamu telah mengetahui bahwa fungsi dinotasikan dengan huruf kecil, seperti f, g, atau h. Pada fungsi f dari himpunan A ke himpunan B, jika x B maka peta atau bayangan x oleh f dinotasikan dengan f (x). Perhatikan Gambar 2.7 . Gambar tersebut menunjukkan fungsi himpunan A ke himpunan B menurut aturan f : x → 2x + 1. Pada gambar, dapat dilihat bahwa x merupakan anggota domain f. Fungsi f : x → 2x + 1 berarti fungsi f memetakan x ke 2x + 1. Oleh karena itu, bayangan x oleh fungsi f adalah 2x + 1. Jadi, dapat dikatakan bahwa f (x) = 2x + 1 adalah rumus untuk fungsi f.Jika fungsi f : x → ax + b dengan x anggota domain f, rumus
fungsi f adalah f (x) = ax + b.
2. Menghitung Nilai Fungsi
Pada bagian ini, kamu akan mempelajari cara menghitung nilai fungsi. Pelajarilah contoh-contoh soal berikut.| Contoh Soal : Diketahui fungsi f: x → 2x – 2 pada himpunan bilangan bulat. Tentukan: a. f (1), b. f (2), c. bayangan (–2) oleh f, d. nilai f untuk x = –5, e. nilai x untuk f (x) = 8, f. nilai a jika f (a) = 14. Jawab : Diketahui f: x → 2x – 2 pada himpunan bilangan bulat. Dengan demikian rumus fungsinya f (x) = 2x –2. a. f (1) = 2 (1) – 2 = 0 b. f (2) = 2 (2) – 2 = 2 c. Bayangan (–2) oleh f sama dengan f (–2). Jadi, f (–2) = 2 (–2) – 2 = –6 d. Nilai f untuk x = –5 adalah f (–5) = 2 (–5) – 2 = –12 e. Nilai x untuk f (x) = 8 adalah 2x – 2 = 8 2x = 8 + 2 2x = 10 x = 5 f. Nilai a jika f (a) = 14 adalah 2a – 2 = 14 2a = 14 + 2 2a = 16 a = 8 Contoh Soal : Diketahui g: x → x2 + 2 dengan domain {x | – 4 < x ≤ 2, x bilangan bulat} dan kodomain bilangan bulat. a. Tuliskan rumus untuk fungsi g. b. Tuliskan domain g dengan mendaftar anggota-anggotanya. c. Tentukan daerah hasil g. d. Gambarlah grafik fungsi g jika domainnya { x | – 4 < x ≤ 1, x bilangan riil} dan kodomainnya diperluas pada himpunan bilangan riil. Jawab : a. Rumus untuk fungsi g adalah g(x) = x2 + 2 b. Domain g adalah Dg = { –3, –2, –1, 0, 1, 2} c. Daerah hasil g: g(x) = x2 + 2 g (–3) = (–3)2 + 2 = 11 g (–2) = (–2)2 + 2 = 6 g (–1) = (–1)2 + 2 = 3 g (0) = (0)2 + 2 = 2 g (1) = (1)2 + 2 = 3 g (2) = (2)2 + 2 = 6 Jadi, daerah hasil g adalah Rg = {2, 3, 6, 11} d. Jika domainnya diketahui{ x | –4 < x ≤ 1, x bilangan riil} dan kodomainnya diperluas pada himpunan bilangan riil, grafiknya seperti pada gambar di samping. |
3. Menentukan Rumus fungsi
Suatu fungsi dapat ditentukan rumusnya jika nilai data diketahui.
Bagaimanakah caranya? Untuk menjawabnya, pelajarilah contoh soal
berikut.| Contoh Soal :
Fungsi h pada himpunan bilangan riil ditentukan oleh rumus h(x) = a x + b, dengan a dan b bilangan bulat. Jika h (–2) = –4 dan h(1) = 5, tentukan: a. nilai a dan b, b. rumus fungsi tersebut. Jawab : h(x) = ax +b a. Oleh karena h(–2) = –4 maka h(–2) = a(–2) + b = –4 –2a + b = –4 …(1) h(1) = 5 maka h(1) = a (1) + b = 5 a + b = 5 b = 5 – a …(2) Substitusikan persamaan (2) ke persamaan (1), diperoleh: –2a + b = –4 –2a + (5 – a) = –4 –2a + 5 – a = –4 –3a + 5 = –4 –3a = –9 a = 3 Substitusikan nilai a = 3 ke persamaan (2), diperoleh b = 5 – a = 5 – 3 = 2 Jadi, nilai a sama dengan 3 dan nilai b sama dengan 2. b. Oleh karena nilai a = 3 dan nilai b = 2, rumus fungsinya adalah h(x) = 3x + 2. |
Subscribe to:
Komentar (Atom)
About
Designed by SkinCorner Free Blogger Templates | Sponsored by Papercraft for Kids | Power Point Templates